关于算法的使用

• 如何看待算法
• 名词介绍
  • 比较(Compare)和交换(Swap)
  • O(N)
  • 时间复杂度和空间复杂度
  • 最坏(Worst)/平均(Average)情况
  • 稳定排序
  • 平均分布
• 常用算法的使用场景浅谈
  • 排序算法
    • 1.冒泡排序(Bubble sort):
    • 2.插入排序(Insertion sort)：
    • 3.选择排序(Selection sort)：
    • 4.快速排序(Quick sort)：
    • 5.堆排序(Heap sort)：
    • 6.归并排序(Merge sort)
    • 7.基数排序(Radix sort)：
    • 8.桶子排序(Bucket sort)：
    • 9.计数排序(Counting sort)：
  • 实战例子：
  • 查找算法
    • 1.顺序查找(sequential search)
    • 2.二分查找(binary search)
    • 3.分块查找(block search)
    • 4.哈希查找(hash search)
    • 5.数据库(Database)
    • 6.搜索引擎(Search engine)
• 常见的时间复杂度
• 文章所提及的算法的baidu地址
• 参考资料

如何看待算法

一个算法如果不会用，其实也不用学了，反正学完也会忘记。所以学习算法最关键的不是怎么写，而是为什么要用，什么时候用，什么时候不该用。等到需要用这个算法的时候，再去google、baidu查就可以了。

名词介绍

比较(Compare)和交换(Swap)

比较：两个字符的大小比较

交换：两个字符的位置交换

O(N)

N代表数据量

大O符号：代表上界

除此之外还有，

大Ω符号：代表下界

大Θ符号：代表上界跟下界刚好相等

但算法上我们通常只在乎 O (读音 Big O)。毕竟 Ω 这种最少需要花费多少时间/空间，并不是我们所关心的。

时间复杂度和空间复杂度

时间复杂度

算法的时间复杂度也就是算法的时间量度，记作T(n)=O(f(n)),T(n)是语句总的执行次数也可以称为执行时间，f(n)是问题规模n的某个函数，算法执行时间T(n)的增长率和f(n)的增长率相同

int i,sum=0,n=100 ;//执行1次
for(int i=1;i<n;i++){//执行了n+1次
    sum=sum+i; //执行n次
}

以上总的执行次数：1+n+1+n可推导该时间复杂度为：O(n)

空间复杂度

计算除正常占用内存开销外的算法所需要的存储空间，记作S(n)=O(f(n)),n为问题的规模，f(n)语句关于n所占的存储空间的函数。

注意：O(N) 在超过一定规模时候，基本上这个算法花费的时间(或是空间)会跟数据量N成正相关。也就是说如果N增加 3 倍，花费的时间/空间也会增加3倍。

最坏(Worst)/平均(Average)情况

平均情况就是我们期望的合理运行时间

最坏情况就是出现最糟糕情况的运行时间

例如：查找一个有n个随机数字数组中的某个数字，最好的情况就是第一个数字，即O(1)，最坏的情况就是最后一个数字，即O(n)。

稳定排序

待排序的记录序列中可能存在两个或两个以上关键字相等的记录。排序前的序列中Ri领先于Rj（即i<j）,若在排序后的序列中Ri仍然领先于Rj，则称所用的方法是稳定的。

平均分布

数据平均在某个范围，数据的变动范围不大

常用算法的使用场景浅谈

排序算法

1.冒泡排序(Bubble sort):

时间复杂度: O(N2次方)

Bubble sort不适合的情况:

几乎所有的正常状况都不适合的情况

Bubble sort适合的情况:

也许小数据量，可以考虑用改良过的 Bubble sort

2.插入排序(Insertion sort)：

时间复杂度: O(N2次方)

Insertion sort不适合的情况:

数据量稍大(或许超过100)

Insertion sort适合的情况:

• 小数据量 (约几十个)直接用Insertion

• 已经快要排好的 Array 可以接近 Best 情况 O(N)

3.选择排序(Selection sort)：

时间复杂度: O(N2次方)

Selection sort不适合的情况:

数据量稍大(或许超过100)

Selection sort适合的情况:

• Selection 是所有排序里面 swap 次数最少的，所以当 swap 代价很高的时候，例如：

  • 每次 swap 要刷新窗口或重新画图

  • 每次 swap 要 swap 数百Mb（兆）的 data

  • 每次 swap 要去 database 记录一次 log（日记）

注1：实际测试数据：如果N=200，且每次 swap 就要刷新，Selection sort 大概比 Quick sort 快 80% ~ 100%)

注2：但N 太大的时候可能抵消 Selection 的优势，要自行斟酌

4.快速排序(Quick sort)：

没有其它排序算法适合的情况的情况下的选择

时间复杂度: O (NlgN)

quick sort不适合的情况:

• 几乎已经排好序的数组

• Array data 接近反向排列

• 需要保证稳定排序的状况

quick sort适合的情况:

• 绝大部分的状况

• 多种编程语言提供了quick sort的方法，如：java中Arrays.sort()对基本类型排序时如果数量大于7则就是使用快速排序

5.堆排序(Heap sort)：

正常情况下比基本上比 Quick sort 要慢

时间复杂度: O (NlgN)

Heap sort不适合的情况:

• 需要保证稳定排序的状况

Heap sort适合的情况:

建议在优先队列里使用，原因如下：

• Heap 建立好之后，取出一个 max/min 只需要 O(lgN) 的时间

• Insert 一次也只需要 O(lgN) 的时间

• 在常变动的环境下，随时想要取得【目前最大 K 个 value】

6.归并排序(Merge sort)

对大数据量进行排序，数据量大到不能全部读进内存里，必须在内存和外存间换进换出进行排序。Merge sort 速度仅次于 Quick sort

时间复杂度： O (NlgN)

空间复杂度： O (N)

Merge sort不适合的情况:

在内存紧缺情况同时数据量不多

Merge sort适合的情况:

• 需要稳定排序

• 需要要 merge 两个/多个 sorted list （有序列表）

• 数据量极大，内存一定不够时 ,Merge sort 可以当作外部排序，每次只读取两个 lists 的前面一小段

• 平行运算（同时使用多台计算资源解决计算问题的过程）

7.基数排序(Radix sort)：

K表示最大的数的位数，N表示多少个数

时间复杂度: O(KN)

空间复杂度 O(K+N)

Radix sort不适合的情况:

• K 没有比 N 小多少 (例如：排序 DNA / RNA就不适合了)

• 位数(长度)变动太大的 data

• Data 每个位数变化太多 ，如：中文姓名

• 数字排序运算上有太多的 % 跟 *

Radix sort适合的情况:

• 数据量多，且固定格式的文字数字 (例如身份证号，邮编，手机号码)

• 数据量多，长度差不多的文字、数字 (英文单字)

8.桶子排序(Bucket sort)：

用 N 个数字，K 个桶子表示

Best & Average 情况: O(K+N)

Worst 情况: O(N2次方)

Bucket 不适合的情况:

• 分布很不平均 (例如：学生成绩为就是平均分布)

• 对空间要求较高 (Bucket sort 非常耗费控件)

• M 型分布

Bucket 适合的情况:

• 分类 (例如要把 e-mail 按照 domain 分开)，但这好像不算排序

• 平均分布时速度极快

9.计数排序(Counting sort)：

花费时间为: O(N+K)

Counting 不适合的情况:

• 非数字

• 大范围数字 (需要超大的 counting array)

• 对空间要求较高 (需要额外 array 储存 counting 以及排序结果)

Counting 适合的情况:

• 小范围数字

实战例子：

查找算法

1.顺序查找(sequential search)

Average 情况: O(N)

quential search 适合的情况:

小数据量(几十、几百)

2.二分查找(binary search)

Average 情况: O(lgN)

binary search适合的情况:

• 大数据量(几千万以下),且已经排序好

• 不经常变动而查找频繁

3.分块查找(block search)

分块查找是折半查找和顺序查找的一种改进方法，需要对数组进行分块，分块查找需要建立一个“索引表”。索引表分为m块，每块含有N/m个元素，块内是无序的，块间是有序的，例如块2中最大元素小于块3中最小元素。

Average 情况: O(log(m)+N/m)

block search适合的情况:

• 大数据量(几千万以下),且块间是有序

• 节点动态变化(当增加或减少节以及节点的关键码改变时，只需将该节点调整到所在的块即可)，但变化不频繁。

4.哈希查找(hash search)

Average 情况: O(1)

hash search适合的情况:

• 大数据量(几千万以下)，且杂乱无排序

5.数据库(Database)

数据库主要是存储数据用，在数据库查找数据主要是通过sql来筛选

Database适合的情况:

• 结构化的数据，数据量最好不要超过百万

6.搜索引擎(Search engine)

Search engine适合的情况:

• 极大的数据量(几千万，几亿)

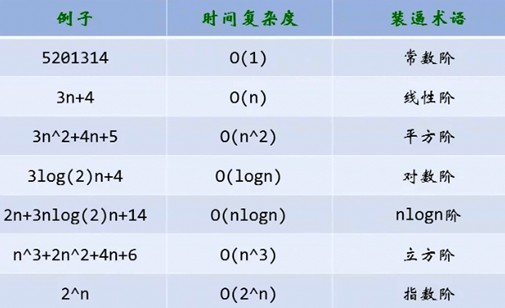
常见的时间复杂度

文章所提及的算法的baidu地址

排序算法 、插入排序、选择排序

快速排序、堆排序、归并排序

基数排序、桶排序、计数排序

哈希查找、顺序查找、二分查找、分块查找

参考资料

1.翁嘉颀-Algorithm算法精讲视频